Signature Calculations for the Authorization Header: Transferring Payload in a Single Chunk (Amazon Signature Version 4) - Amazon Simple Storage Service
Calculating a Signature
Services or capabilities described in Amazon Web Services documentation might vary by Region. To see the differences applicable to the China Regions, see Getting Started with Amazon Web Services in China (PDF).

Signature Calculations for the Authorization Header: Transferring Payload in a Single Chunk (Amazon Signature Version 4)

When using the Authorization header to authenticate requests, the header value includes, among other things, a signature. The signature calculations vary depending on the choice you make for transferring the payload (Overview). This section explains signature calculations when you choose to transfer the payload in a single chunk. The example section (see Examples: Signature Calculations) shows signature calculations and resulting Authorization headers that you can use as a test suite to verify your code.

Important

When transferring payload in a single chunk, you can optionally choose to include the payload hash in the signature calculations, referred as signed payload (if you don't include it, the payload is considered unsigned). The signing procedure discussed in the following section applies to both, but note the following differences:

  • Signed payload option – You include the payload hash when constructing the canonical request (that then becomes part of StringToSign, as explained in the signature calculation section). You also specify the same value as the x-amz-content-sha256 header value when sending the request to S3.

  • Unsigned payload option – You include the literal string UNSIGNED-PAYLOAD when constructing a canonical request, and set the same value as the x-amz-content-sha256 header value when sending the request to Amazon S3.

When you send your request to Amazon S3, the x-amz-content-sha256 header value informs Amazon S3 whether the payload is signed or not. Amazon S3 can then create the signature accordingly for verification.

Calculating a Signature

To calculate a signature, you first need a string to sign. You then calculate a HMAC-SHA256 hash of the string to sign by using a signing key. The following diagram illustrates the process, including the various components of the string that you create for signing

When Amazon S3 receives an authenticated request, it computes the signature and then compares it with the signature that you provided in the request. For that reason, you must compute the signature by using the same method that is used by Amazon S3. The process of putting a request in an agreed-upon form for signing is called canonicalization.

Amazon Signature Version 4 process diagram showing Canonical Request, StringToSign, and Signature steps.

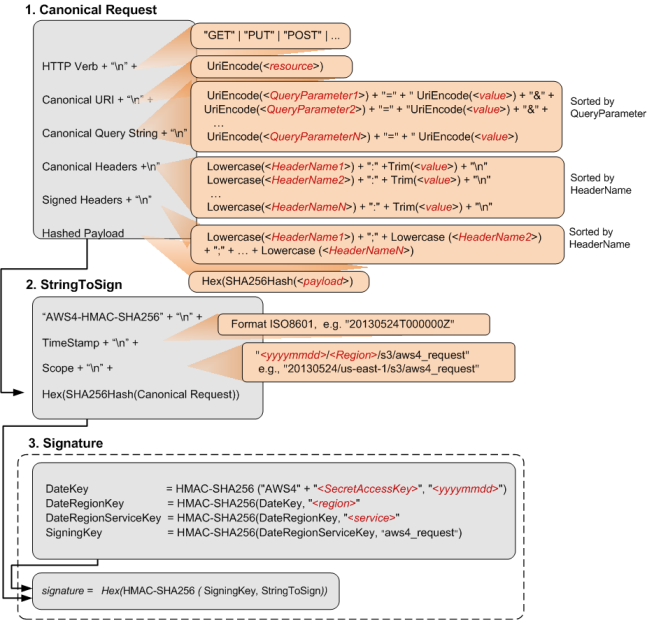
The following table describes the functions that are shown in the diagram. You need to implement code for these functions.

Function Description
Lowercase() Convert the string to lowercase.
Hex() Lowercase base 16 encoding.
SHA256Hash() Secure Hash Algorithm (SHA) cryptographic hash function.
HMAC-SHA256() Computes HMAC by using the SHA256 algorithm with the signing key provided. This is the final signature.
Trim() Remove any leading or trailing whitespace.
UriEncode()

URI encode every byte. UriEncode() must enforce the following rules:

  • URI encode every byte except the unreserved characters: 'A'-'Z', 'a'-'z', '0'-'9', '-', '.', '_', and '~'.

  • The space character is a reserved character and must be encoded as "%20" (and not as "+").

  • Each URI encoded byte is formed by a '%' and the two-digit hexadecimal value of the byte.

  • Letters in the hexadecimal value must be uppercase, for example "%1A".

  • Encode the forward slash character, '/', everywhere except in the object key name. For example, if the object key name is photos/Jan/sample.jpg, the forward slash in the key name is not encoded.

Important

The standard UriEncode functions provided by your development platform may not work because of differences in implementation and related ambiguity in the underlying RFCs. We recommend that you write your own custom UriEncode function to ensure that your encoding will work.

To see an example of a UriEncode function in Java, see Java Utilities on the GitHub website.

Task 1: Create a Canonical Request

This section provides an overview of creating a canonical request.

The following is the canonical request format that Amazon S3 uses to calculate a signature. For signatures to match, you must create a canonical request in this format: 

<HTTPMethod>\n
<CanonicalURI>\n
<CanonicalQueryString>\n
<CanonicalHeaders>\n
<SignedHeaders>\n
<HashedPayload>

Where:

  • HTTPMethod is one of the HTTP methods, for example GET, PUT, HEAD, and DELETE.

  • CanonicalURI is the URI-encoded version of the absolute path component of the URI—everything starting with the "/" that follows the domain name and up to the end of the string or to the question mark character ('?') if you have query string parameters. The URI in the following example, /examplebucket/myphoto.jpg, is the absolute path and you don't encode the "/" in the absolute path:

    http://s3.amazonaws.com/examplebucket/myphoto.jpg

    Note

    You do not normalize URI paths for requests to Amazon S3. For example, you may have a bucket with an object named "my-object//example//photo.user". Normalizing the path changes the object name in the request to "my-object/example/photo.user". This is an incorrect path for that object.

  • CanonicalQueryString specifies the URI-encoded query string parameters. You URI-encode name and values individually. You must also sort the parameters in the canonical query string alphabetically by key name. The sorting occurs after encoding. The query string in the following URI example is prefix=somePrefix&marker=someMarker&max-keys=20:

    http://s3.amazonaws.com/examplebucket?prefix=somePrefix&marker=someMarker&max-keys=20

    The canonical query string is as follows (line breaks are added to this example for readability):

    UriEncode("marker")+"="+UriEncode("someMarker")+"&"+
UriEncode("max-keys")+"="+UriEncode("20") + "&" +
UriEncode("prefix")+"="+UriEncode("somePrefix")

    When a request targets a subresource, the corresponding query parameter value will be an empty string (""). For example, the following URI identifies the ACL subresource on the examplebucket bucket:

    http://s3.amazonaws.com/examplebucket?acl

    The CanonicalQueryString in this case is as follows:

    UriEncode("acl") + "=" + ""

    If the URI does not include a '?', there is no query string in the request, and you set the canonical query string to an empty string (""). You will still need to include the "\n".

  • CanonicalHeaders is a list of request headers with their values. Individual header name and value pairs are separated by the newline character ("\n"). Header names must be in lowercase. You must sort the header names alphabetically to construct the string, as shown in the following example:

    Lowercase(<HeaderName1>)+":"+Trim(<value>)+"\n"
Lowercase(<HeaderName2>)+":"+Trim(<value>)+"\n"
...
Lowercase(<HeaderNameN>)+":"+Trim(<value>)+"\n"

    The Lowercase() and Trim() functions used in this example are described in the preceding section.

    The CanonicalHeaders list must include the following:

    • HTTP host header.

    • If the Content-MD5 header is present in the request, you must add it to the CanonicalHeaders list.

    • Any x-amz-* headers that you plan to include in your request must also be added. For example, if you are using temporary security credentials, you need to include x-amz-security-token in your request. You must add this header in the list of CanonicalHeaders.

    Note

    The x-amz-content-sha256 header is required for all Amazon Signature Version 4 requests. It provides a hash of the request payload. If there is no payload, you must provide the hash of an empty string.

    The following is an example CanonicalHeaders string. The header names are in lowercase and sorted.

    host:s3.amazonaws.com
x-amz-content-sha256:e3b0c44298fc1c149afbf4c8996fb92427ae41e4649b934ca495991b7852b855
x-amz-date:20130708T220855Z

    Note

    For the purpose of calculating an authorization signature, only the host and any x-amz-* headers are required; however, in order to prevent data tampering, you should consider including all the headers in the signature calculation.

  • SignedHeaders is an alphabetically sorted, semicolon-separated list of lowercase request header names. The request headers in the list are the same headers that you included in the CanonicalHeaders string. For example, for the previous example, the value of SignedHeaders would be as follows:

    host;x-amz-content-sha256;x-amz-date

  • HashedPayload is the hexadecimal value of the SHA256 hash of the request payload. 

    Hex(SHA256Hash(<payload>)

    If there is no payload in the request, you compute a hash of the empty string as follows:

    Hex(SHA256Hash(""))

    The hash returns the following value:

    e3b0c44298fc1c149afbf4c8996fb92427ae41e4649b934ca495991b7852b855

    For example, when you upload an object by using a PUT request, you provide object data in the body. When you retrieve an object by using a GET request, you compute the empty string hash.

Task 2: Create a String to Sign

This section provides an overview of creating a string to sign. For step-by-step instructions, see Task 2: Create a String to Sign in the Amazon Web Services General Reference.

The string to sign is a concatenation of the following strings:

"AWS4-HMAC-SHA256" + "\n" +
timeStampISO8601Format + "\n" +
<Scope> + "\n" +
Hex(SHA256Hash(<CanonicalRequest>))

The constant string AWS4-HMAC-SHA256 specifies the hash algorithm that you are using, HMAC-SHA256. The timeStamp is the current UTC time in ISO 8601 format (for example, 20130524T000000Z).

Scope binds the resulting signature to a specific date, an Amazon Web Services Region, and a service. Thus, your resulting signature will work only in the specific Region and for a specific service. The signature is valid for seven days after the specified date.

date.Format(<YYYYMMDD>) + "/" + <region> + "/" + <service> + "/aws4_request"

For Amazon S3, the service string is s3. For a list of region strings, see Regions and Endpoints in the Amazon Web Services General Reference. The Region column in this table provides the list of valid Region strings.

The following scope restricts the resulting signature to the us-east-1 Region and Amazon S3. 

20130606/us-east-1/s3/aws4_request

Note

Scope must use the same date that you use to compute the signing key, as discussed in the following section.

Task 3: Calculate Signature

In Amazon Signature Version 4, instead of using your Amazon access keys to sign a request, you first create a signing key that is scoped to a specific Region and service.  For more information about signing keys, see Introduction to Signing Requests. 

DateKey              = HMAC-SHA256("AWS4"+"<SecretAccessKey>", "<YYYYMMDD>")
DateRegionKey        = HMAC-SHA256(<DateKey>, "<aws-region>")
DateRegionServiceKey = HMAC-SHA256(<DateRegionKey>, "<aws-service>")
SigningKey           = HMAC-SHA256(<DateRegionServiceKey>, "aws4_request")

Note

Some use cases can process signature keys for up to 7 days. For more information see Share an Object with Others.

For a list of Region strings, see Regions and Endpoints in the Amazon Web Services General Reference.

Using a signing key enables you to keep your Amazon credentials in one safe place. For example, if you have multiple servers that communicate with Amazon S3, you share the signing key with those servers; you don’t have to keep a copy of your secret access key on each server. Signing key is valid for up to seven days. So each time you calculate signing key you will need to share the signing key with your servers. For more information, see Authenticating Requests (Amazon Signature Version 4).

The final signature is the HMAC-SHA256 hash of the string to sign, using the signing key as the key.

HMAC-SHA256(SigningKey, StringToSign)

For step-by-step instructions on creating a signature, see Task 3: Create a Signature in the Amazon Web Services General Reference.

Examples: Signature Calculations

You can use the examples in this section as a reference to check signature calculations in your code. The calculations shown in the examples use the following data:

  • Example access keys.

    Parameter Value
    AWSAccessKeyId AKIAIOSFODNN7EXAMPLE
    AWSSecretAccessKey wJalrXUtnFEMI/K7MDENG/bPxRfiCYEXAMPLEKEY

  • Request timestamp of 20130524T000000Z (Fri, 24 May 2013 00:00:00 GMT).

  • Bucket name examplebucket.

  • The bucket is assumed to be in the US East (N. Virginia) Region. The credential Scope and the Signing Key calculations use us-east-1 as the Region specifier. For information about other Regions, see Regions and Endpoints in the Amazon Web Services General Reference.

  • You can use either path-style or virtual hosted–style requests. The following examples show how to sign a virtual hosted–style request, for example:

    https://examplebucket.s3.amazonaws.com/photos/photo1.jpg

    For more information, see Virtual Hosting of Buckets in the Amazon Simple Storage Service User Guide.

Example: GET Object

The following example gets the first 10 bytes of an object (test.txt) from examplebucket. For more information about the API action, see GetObject.

GET /test.txt HTTP/1.1
Host: examplebucket.s3.amazonaws.com
Authorization: SignatureToBeCalculated
Range: bytes=0-9 
x-amz-content-sha256:e3b0c44298fc1c149afbf4c8996fb92427ae41e4649b934ca495991b7852b855
x-amz-date: 20130524T000000Z

Because this GET request does not provide any body content, the x-amz-content-sha256 value is the hash of the empty request body. The following steps show signature calculations and construction of the Authorization header.

  1. StringToSign
    1. CanonicalRequest

      GET
/test.txt

host:examplebucket.s3.amazonaws.com
range:bytes=0-9
x-amz-content-sha256:e3b0c44298fc1c149afbf4c8996fb92427ae41e4649b934ca495991b7852b855
x-amz-date:20130524T000000Z

host;range;x-amz-content-sha256;x-amz-date
e3b0c44298fc1c149afbf4c8996fb92427ae41e4649b934ca495991b7852b855

      In the canonical request string, the last line is the hash of the empty request body. The third line is empty because there are no query parameters in the request.

    2. StringToSign

      AWS4-HMAC-SHA256
20130524T000000Z
20130524/us-east-1/s3/aws4_request
7344ae5b7ee6c3e7e6b0fe0640412a37625d1fbfff95c48bbb2dc43964946972

  2. SigningKey

    signing key = HMAC-SHA256(HMAC-SHA256(HMAC-SHA256(HMAC-SHA256("AWS4" + "<YourSecretAccessKey>","20130524"),"us-east-1"),"s3"),"aws4_request")

  3. Signature

    f0e8bdb87c964420e857bd35b5d6ed310bd44f0170aba48dd91039c6036bdb41

  4. Authorization header

    The resulting Authorization header is as follows: 

    AWS4-HMAC-SHA256 Credential=AKIAIOSFODNN7EXAMPLE/20130524/us-east-1/s3/aws4_request,SignedHeaders=host;range;x-amz-content-sha256;x-amz-date,Signature=f0e8bdb87c964420e857bd35b5d6ed310bd44f0170aba48dd91039c6036bdb41

Example: PUT Object

This example PUT request creates an object (test$file.text) in examplebucket . The example assumes the following:

  • You are requesting REDUCED_REDUNDANCY as the storage class by adding the x-amz-storage-class request header. For information about storage classes, see Storage Classes in the Amazon Simple Storage Service User Guide.

  • The content of the uploaded file is a string, "Welcome to Amazon S3." The value of x-amz-content-sha256 in the request is based on this string.

For information about the API action, see PutObject. 

PUT test$file.text HTTP/1.1
Host: examplebucket.s3.amazonaws.com
Date: Fri, 24 May 2013 00:00:00 GMT
Authorization: SignatureToBeCalculated
x-amz-date: 20130524T000000Z 
x-amz-storage-class: REDUCED_REDUNDANCY
x-amz-content-sha256: 44ce7dd67c959e0d3524ffac1771dfbba87d2b6b4b4e99e42034a8b803f8b072

<Payload>

The following steps show signature calculations.

  1. StringToSign
    1. CanonicalRequest

      PUT
/test%24file.text

date:Fri, 24 May 2013 00:00:00 GMT
host:examplebucket.s3.amazonaws.com
x-amz-content-sha256:44ce7dd67c959e0d3524ffac1771dfbba87d2b6b4b4e99e42034a8b803f8b072
x-amz-date:20130524T000000Z
x-amz-storage-class:REDUCED_REDUNDANCY

date;host;x-amz-content-sha256;x-amz-date;x-amz-storage-class
44ce7dd67c959e0d3524ffac1771dfbba87d2b6b4b4e99e42034a8b803f8b072

      In the canonical request, the third line is empty because there are no query parameters in the request. The last line is the hash of the body, which should be same as the x-amz-content-sha256 header value.

    2. StringToSign

      AWS4-HMAC-SHA256
20130524T000000Z
20130524/us-east-1/s3/aws4_request
9e0e90d9c76de8fa5b200d8c849cd5b8dc7a3be3951ddb7f6a76b4158342019d

  2. SigningKey

    signing key = HMAC-SHA256(HMAC-SHA256(HMAC-SHA256(HMAC-SHA256("AWS4" + "<YourSecretAccessKey>","20130524"),"us-east-1"),"s3"),"aws4_request")

  3. Signature

    98ad721746da40c64f1a55b78f14c238d841ea1380cd77a1b5971af0ece108bd

  4. Authorization header

    The resulting Authorization header is as follows:

    AWS4-HMAC-SHA256 Credential=AKIAIOSFODNN7EXAMPLE/20130524/us-east-1/s3/aws4_request,SignedHeaders=date;host;x-amz-content-sha256;x-amz-date;x-amz-storage-class,Signature=98ad721746da40c64f1a55b78f14c238d841ea1380cd77a1b5971af0ece108bd

Example: GET Bucket Lifecycle

The following GET request retrieves the lifecycle configuration of examplebucket. For information about the API action, see GetBucketLifecycleConfiguration. 

GET ?lifecycle HTTP/1.1
Host: examplebucket.s3.amazonaws.com
Authorization: SignatureToBeCalculated
x-amz-date: 20130524T000000Z 
x-amz-content-sha256:e3b0c44298fc1c149afbf4c8996fb92427ae41e4649b934ca495991b7852b855

Because the request does not provide any body content, the x-amz-content-sha256 header value is the hash of the empty request body. The following steps show signature calculations.

  1. StringToSign
    1. CanonicalRequest

      GET
/
lifecycle=
host:examplebucket.s3.amazonaws.com
x-amz-content-sha256:e3b0c44298fc1c149afbf4c8996fb92427ae41e4649b934ca495991b7852b855
x-amz-date:20130524T000000Z

host;x-amz-content-sha256;x-amz-date
e3b0c44298fc1c149afbf4c8996fb92427ae41e4649b934ca495991b7852b855

      In the canonical request, the last line is the hash of the empty request body.

    2. StringToSign

      AWS4-HMAC-SHA256
20130524T000000Z
20130524/us-east-1/s3/aws4_request
9766c798316ff2757b517bc739a67f6213b4ab36dd5da2f94eaebf79c77395ca

  2. SigningKey

    signing key = HMAC-SHA256(HMAC-SHA256(HMAC-SHA256(HMAC-SHA256("AWS4" + "<YourSecretAccessKey>","20130524"),"us-east-1"),"s3"),"aws4_request")

  3. Signature

    fea454ca298b7da1c68078a5d1bdbfbbe0d65c699e0f91ac7a200a0136783543

  4. Authorization header

    The resulting Authorization header is as follows: 

    AWS4-HMAC-SHA256 Credential=AKIAIOSFODNN7EXAMPLE/20130524/us-east-1/s3/aws4_request,SignedHeaders=host;x-amz-content-sha256;x-amz-date,Signature=fea454ca298b7da1c68078a5d1bdbfbbe0d65c699e0f91ac7a200a0136783543

Example: Get Bucket (List Objects)

The following example retrieves a list of objects from examplebucket bucket. For information about the API action, see ListObjects. 

GET ?max-keys=2&prefix=J HTTP/1.1
Host: examplebucket.s3.amazonaws.com
Authorization: SignatureToBeCalculated
x-amz-date: 20130524T000000Z 
x-amz-content-sha256:e3b0c44298fc1c149afbf4c8996fb92427ae41e4649b934ca495991b7852b855

Because the request does not provide a body, the value of x-amz-content-sha256 is the hash of the empty request body. The following steps show signature calculations.

  1. StringToSign
    1. CanonicalRequest

      GET
/
max-keys=2&prefix=J
host:examplebucket.s3.amazonaws.com
x-amz-content-sha256:e3b0c44298fc1c149afbf4c8996fb92427ae41e4649b934ca495991b7852b855
x-amz-date:20130524T000000Z

host;x-amz-content-sha256;x-amz-date
e3b0c44298fc1c149afbf4c8996fb92427ae41e4649b934ca495991b7852b855

      In the canonical string, the last line is the hash of the empty request body.

    2. StringToSign

      AWS4-HMAC-SHA256
20130524T000000Z
20130524/us-east-1/s3/aws4_request
df57d21db20da04d7fa30298dd4488ba3a2b47ca3a489c74750e0f1e7df1b9b7

  2. SigningKey

    signing key = HMAC-SHA256(HMAC-SHA256(HMAC-SHA256(HMAC-SHA256("AWS4" + "<YourSecretAccessKey>","20130524"),"us-east-1"),"s3"),"aws4_request")

  3. Signature

    34b48302e7b5fa45bde8084f4b7868a86f0a534bc59db6670ed5711ef69dc6f7

  4. Authorization header

    The resulting Authorization header is as follows: 

    AWS4-HMAC-SHA256 Credential=AKIAIOSFODNN7EXAMPLE/20130524/us-east-1/s3/aws4_request,SignedHeaders=host;x-amz-content-sha256;x-amz-date,Signature=34b48302e7b5fa45bde8084f4b7868a86f0a534bc59db6670ed5711ef69dc6f7