PCA 工作原理 - 亚马逊 SageMaker AI
模式 1：常规模式 2：随机
Amazon Web Services 文档中描述的 Amazon Web Services 服务或功能可能因区域而异。要查看适用于中国区域的差异，请参阅 中国的 Amazon Web Services 服务入门 (PDF)。

本文属于机器翻译版本。若本译文内容与英语原文存在差异，则一律以英文原文为准。

PCA 工作原理

主成分分析 (PCA) 是一种自主型机器学习算法，它在数据集内减少维数 (特征个数)，同时仍保留尽可能多的信息。

PCA 通过查找称为成分的新特征集减少维数，这些功能是原始特征的复合体，但彼此不相关。第一个成分在数据中可能存在最大的可变性，第二个成分是第二个最易变的，以此类推。

它是一种自主型维数减少算法。在自主学习中，不使用可能与训练数据集中的对象相关联的标签。

假定输入中的矩阵包含行 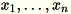x_1,…,x_n ，每个行具有维度 1 * d，数据将被分成小批量行，并分布到训练节点（工作线程）中。然后，每个工作线程计算其数据的摘要。然后在计算结束时，不同工作线程的摘要统一为一个解决方案。

模式

Amazon SageMaker AI PCA 算法使用两种模式中的任何一种来计算这些摘要，具体视情况而定：

  • 常规：针对具有稀疏数据以及适度数量的观察和特征的数据集。

  • 随机：针对具有大量观察和特征的数据集。此模式使用近似算法。

作为算法的最后一步，它在统一解决方案上执行单值分解，然后将会从中导出主成分。

模式 1：常规

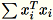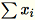工作线程联合计算 Equation in text-form: \sum x_i^T x_i 和 Equation in text-form: \sum x_i 。

注意

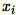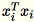由于 Equation in text-form: x_i 为 1 * d 个行向量， Equation in text-form: x_i^T x_i 是一个矩阵（非标量）。在代码中使用行向量可以使我们获得高效的缓存。

协方差矩阵的计算方式为 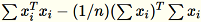Equation in text-form: \sum x_i^T x_i - (1/n) (\sum x_i)^T \sum x_i ，其最前面的 num_components 个奇异向量构成模型。

注意

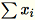如果 subtract_mean 是 False，我们会避免计算和减去 Equation in text-form: \sum x_i 。

当满足以下条件时使用此算法：向量的维度 d 足够小，以致 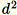Equation in text-form: d^2 可以放入内存中。

模式 2：随机

当输入数据集中的特征数量较大时，我们使用一个方法来近似计算协方差指标。对于维度 b * d 的每个小批量 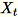Equation in text-form: X_t ，我们随机初始化一个我们与每个小批量相乘的 (num_components + extra_components) * b 矩阵，从而创建一个 (num_components + extra_components) * d 矩阵。这些矩阵的总和由工作线程计算，服务器在最终 (num_components + extra_components) * d 矩阵上执行 SVD。其右上方的 num_components 单向量是输入矩阵的顶部单向量的近似值。

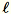
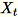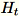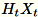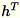指定 Equation in text-form: \ell = num_components + extra_components。假定一个维度 b * d 的小批量 Equation in text-form: X_t ，工作线程会提取维度 Equation in text-form: \ell * b 的随机矩阵 Equation in text-form: H_t 。根据环境是使用 GPU 还是 CPU 以及维度大小，矩阵是随机签名矩阵 (其中每个条目是 +-1) 或 FJLT (快速 Johnson Lindenstrauss 转换；有关信息，请参阅 FJLT 转换跟进文章)。随后工作线程会计算 Equation in text-form: H_t X_t 并维护 Equation in text-form: B = \sum H_t X_t 。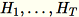工作线程还维护 Equation in text-form: h^T 、 Equation in text-form: H_1,..,H_T （T 为小批量的总数）的列总和以及 s（所有输入行的总和）。在处理完整个数据碎片后，工作线程会向服务器发送 B、h、s 和 n (输入行的数量)。

将不同输入对服务器表示为 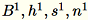Equation in text-form: B^1, h^1, s^1, n^1,… 。服务器会计算 B、h、s、n 的各自输入的总和。然后，它计算 Equation in text-form: C = B – (1/n) h^T s ，并查找其奇异值分解。C 的右上单向量和单值被用作解决问题的近似方法。