本文属于机器翻译版本。若本译文内容与英语原文存在差异,则一律以英文原文为准。
RCF 工作原理
Amazon SageMaker AI Random Cut Forest (RCF) 是一种无监督算法,用于检测数据集中的异常数据点。这些数据点是与良好结构或模式化数据存在偏差的观察数据。异常可以表现为时间序列数据中意外峰值、周期性中断或无法分类的数据点。它们很容易描述,表现为在图中查看时,它们通常很容易与“常规”数据区分。数据集中包括这些异常会显著增加机器学习任务的复杂性,因为“常规”数据通常使用简单模型描述。
RCF 算法的主要理念是创建森林,其中的每棵树使用训练数据样本的一个分区获得。例如,首先确定输入数据的随机样本。然后,根据森林中树的数量对随机样本分区。向每个树提供一个这样的分区,并将这些点的子集整理到 k-d 树中。由树分配给数据点的异常分数定义为将该点添加到树中导致的树的复杂性变化;这大致与点在树中生成的深度成反比。Random Cut Forest 通过从组成的每棵树计算平均分数,并根据样本大小缩放结果,从而分配异常分数。RCF 算法基于引用 [1] 中所述的算法之一。
随机采样数据
RCF 算法的第一步是获取训练数据的随机样本。具体而言,假设我们希望从总共
 个数据点中提取
个数据点中提取
 个数据点的样本。如果训练数据集足够小,可以使用整个数据集,并且我们可以从此数据集随机提取
个数据点的样本。如果训练数据集足够小,可以使用整个数据集,并且我们可以从此数据集随机提取
 个元素。但是,训练数据经常会太大,无法一次使用,此方法不可行。我们改用一种称为水库采样的技术。
个元素。但是,训练数据经常会太大,无法一次使用,此方法不可行。我们改用一种称为水库采样的技术。
水库采样 中有效地提取随机样本,其中数据集中的元素只能观察一次或者批量观察。事实上,即使
中有效地提取随机样本,其中数据集中的元素只能观察一次或者批量观察。事实上,即使
 不是事先知道,水库采样仍可工作。如果只请求一个样本,例如当
不是事先知道,水库采样仍可工作。如果只请求一个样本,例如当
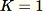 时,算法类似于:
时,算法类似于:
算法:水库采样
-
输入:数据集或数据流

-
初始化随机样本
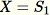
-
对于每个观察到的采样
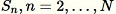 :
:-
选取统一随机号码
![Equation in text-form: \xi \in [0,1]](images/rcf6.jpg)
-
如果
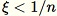
-
Set

-
-
-
返回值
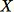
此算法选择随机采样,这样对于所有
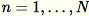 ,可计算
,可计算
 。当
。当
 时,算法更复杂。此外,必须区分使用替换和不使用替换的随机采样。RCF 基于 [2] 中所述的算法,对训练数据执行增强水库采样而不使用替换。
时,算法更复杂。此外,必须区分使用替换和不使用替换的随机采样。RCF 基于 [2] 中所述的算法,对训练数据执行增强水库采样而不使用替换。
训练 RCF 模型和生成推理
RCF 中的下一步是使用随机采样的数据构造 Random Cut Forest。首先,该样本分为多个大小相等的分区,其数量与森林中树的数量相同。然后,每个分区发送到单个树。树通过将数据域分区到边界框,以递归方式将其分区组织到二进制树中。
这个过程可以通过一个例子来很好地说明。假设向一颗树提供了以下二维数据集。对应的树初始化到根节点:
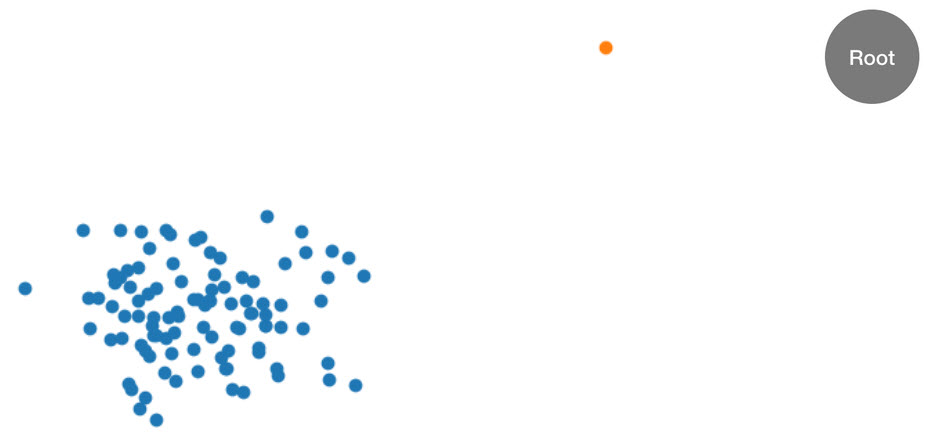
图:一个二维数据集,大多数数据位于集群(蓝色)中,但一个异常数据点(橙色)除外。使用根节点初始化树。
RCF 算法首先计算数据的边界框,选择随机维 (向具有较高“方差”的维提供更多权重),然后通过该维随机确定 Hyperplane“砍伐”的位置,从而将这些数据组织到树中。生成的两个子空间定义自己的子树。在本示例中,通过砍伐将单一点与样本中其余数据分离开。生成的二进制树的第一级包含两个节点,其中一个由初始砍伐左侧点的子树组成,另一个表示右侧的单一点。
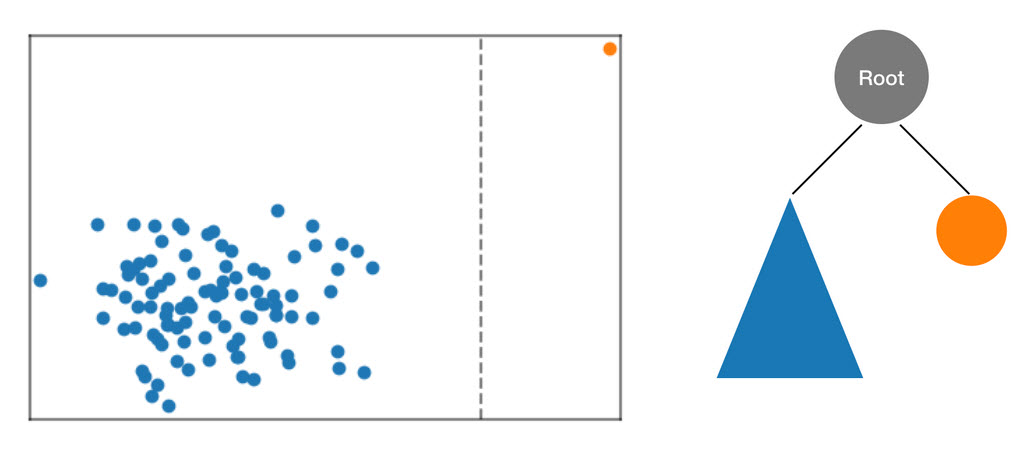
图:随机砍伐对二维数据集分区。异常数据点更可能隔离在边界框中,相比其他点具有较小的树深度。
然后,对两等分的数据计算左侧和右侧的边界框,重复该过程,直至树的每个叶表示来自样本的一个数据点。请注意,如果单一点足够远,则随机砍伐更可能产生点隔离。此观察提供的直觉感受是,大致来说,树深度与异常分数成反比。
使用经过训练的 RCF 模型执行推理时,按照每棵树报告的分数的平均值报告最终异常分数。请注意,经常会出现新的数据点不在树中的情况。要确定与新数据点关联的分数,请将数据点插入指定树中,按照与上述训练过程相等的方式,高效 (并且临时) 重组树。也就是说,就像输入数据点是最初用于构造树时所用样本的成员那样生成了树。报告的分数与输入点在树中的深度成反比。
选择超参数
用于优化 RCF 模型的主要超参数为 num_trees 和 num_samples_per_tree。增加 num_trees 具有减少在异常分数中观察到的噪音的效果,因为最终分数是各个树报告的分数的平均值。尽管最优值取决于应用,我们建议使用 100 个树开始,以在分数噪声和模型复杂性之间取得平衡。请注意,推理时间与树的数量成正比。虽然训练时间也会受影响,但主要由上述的水库采样算法决定。
参数 num_samples_per_tree 与数据集中的预期异常密度相关。具体而言,num_samples_per_tree 的选择应该使得 1/num_samples_per_tree 大致相当于异常数据与普通数据的比率。例如,如果每个树中使用 256 个样本,则我们预期数据包含 1/256 的异常,或者大约为 0.4% 的时间。同样,此超参数的最优值取决于应用。
参考信息
-
Sudipto Guha、Nina Mishra、Gourav Roy 和 Okke Schrijvers。“基于流上异常检测的可靠 Random Cut Forest。” 机器学习国际会议会刊,第 2712-2721 页。2016 年。
-
Byung-Hoon Park、George Ostrouchov、Nagiza F. Samatova 和 Al Geist。“可在数据流中进行替换的基于水库的随机采样。” 2004 年 SIAM 国际数据挖掘会议的会议记录,第 492-496 页。Society for Industrial and Applied Mathematics,2004 年。